Häufigkeiten und Wahrscheinlichkeiten
Häufigkeiten und Wahrscheinlichkeiten – verstehen, lernen und üben


Häufigkeiten und Wahrscheinlichkeiten
- Wahrscheinlichkeiten
- Produktregel
- Summenregel
- LaPlace-Wahrscheinlichkeit
- Boxplots
- Häufigkeiten
Wahrscheinlichkeiten
Wahrscheinlichkeiten ermöglichen es, bei Zufallsexperimenten über das Vorkommen von Ereignissen Vorhersagen machen zu können.
Man unterscheidet einstufige Zufallsexperimente und mehrstufige Zufallsexperimente.
- Einstufiges Zufallsexperiment: Der Zufallsversuch wird nur einmal durchgeführt. Beispiel: eine Münze wird einmal geworfen. Oben erscheint entweder „Kopf“ oder „Zahl“.
- Mehrstufiges Zufallsexperiment: Der Zufallsversuch wird mehrmals (n-mal) durchgeführt. Beispiel: eine Münze wird mehrfach geworfen.
Begriffe der Wahrscheinlichkeitsrechnung:
- Baumdiagramm: die einzelnen Wahrscheinlichkeiten des mehrstufigen Zufallsversuches lässt sich in einem Baumdiagramm darstellen und berechnen.
- Pfad: Der Weg von einer Stufe zur anderen Stufe innerhalb eines Ereignisses bezeichnet man als Pfad.

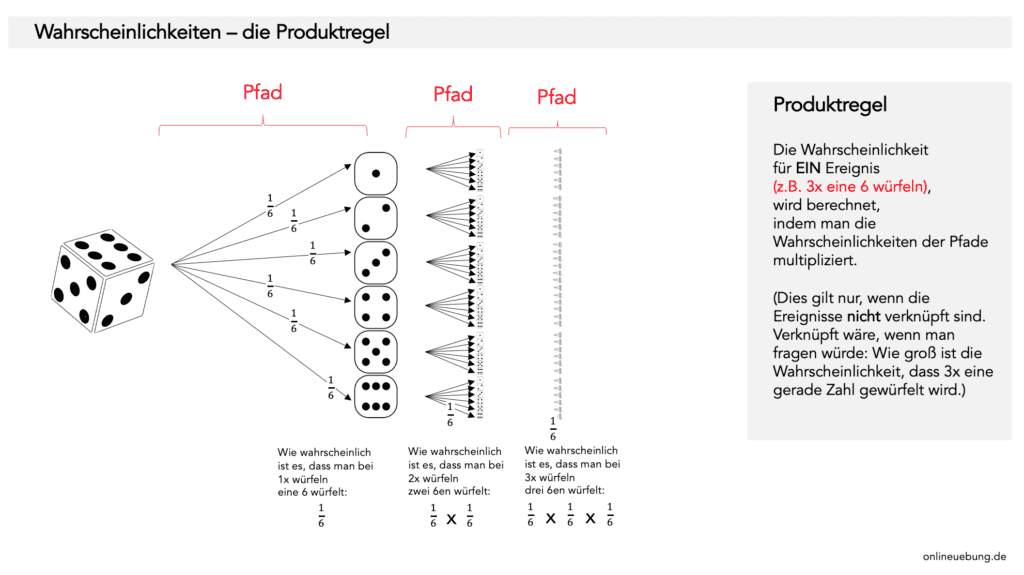
Produktregel
Möchte man die Wahrscheinlichkeit für EIN Ereignis berechnen, werden die Wahrscheinlichkeiten der Pfade multipliziert.
Dies gilt nur, wenn die Ereignisse nicht verknüpft sind. (Verknüpft heißt, mehrere Ereignisse fallen in die Ergebnismenge – siehe Beispiel Münzen: wie groß ist die Wahrscheinlichkeit, dass bei 2x Werfen sich zwei gleiche Ereignisse ergeben – 2x Kopf oder 2x Zahl.)

Summenregel
Führen mehrere Pfade / Stufen zu einem Ereignis, werden die – nach der Produktregel multiplizierten – Wahrscheinlichkeiten addiert.
Die Summe aller Wahrscheinlichkeiten (= Ereignis und Nicht-Ereignis) ist immer 1 – , wenn die Ereignisse verknüpft sind.


LaPlace-Wahrscheinlichkeit
- Definition: Treten alle Ereignisse in einem Zufallsversuch mit gleicher Wahrscheinlichkeit auf, so nennt man die dazugehörigen Wahrscheinlichkeiten Laplace-Wahrscheinlichkeiten. Diesen Versuch nennt man Laplace-Versuch. Sie ist eine Sonderform der Zufallsexperimenten.
- Beispiel: Würfelwurf: Ein Würfel wird 1 mal gewürfelt. Alle 6 Seiten sind gleich groß und können also mit gleicher Wahrscheinlichkeit auftreten.
- Beispiel: Kugeln ziehen: In einer Schale befinden sich 6 gleichgroße Kugeln. Es gibt 3 rote und 3 blaue Kugeln. Die Wahrscheinlichkeit eine rote bzw. eine blaue Kugel zu ziehen ist gleich groß, weil es dieselbe Anzahl an blauen und roten Kugeln gibt und weil die Kugeln alle gleich groß sind.
- Beispiel: Münzwurf: Eine Münze wird 1mal geworfen. Beide Seiten, entweder die Kopfseite oder Zahlseite, können mit gleicher Wahrscheinlichkeit auftreten, da beide Flächen gleich groß sind. Somit wird keine Seite bevorzugt und die beiden Seiten treten mit derselben Wahrscheinlichkeit auf.
- Berechnung der Wahrscheinlichkeit von LaPlace-Experimenten: Anzahl der gewünschten Ereignisse/Anzahl der möglichen Ereignisse
- Beispiel: Münzwurf: Die Kopfseite ist z.B das gewünschte Ereignis und es können im Versuch insgesamt 2 mögliche Ereignisse (Kopf oder Zahl) auftreten. 1/2 = 0,5 = 50%
Boxplots
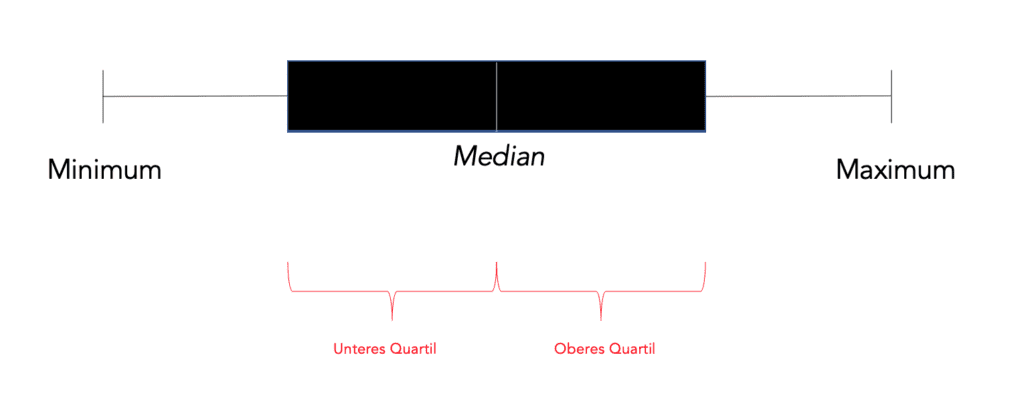
- Definition: Boxplots ermöglichen es, Daten darzustellen. Der Name Box(=Kasten) plot(=zeichnen) sagt schon aus, wobei es sich hier handelt.
- Minimum: Der kleinste Wert, der in der Datensammlung vorkommt. Hier startet die linke Antenne.
- Maximum: Der größte Wert, der in der Datensammlung vorkommt. Hier startet die rechte Antenne.
- Median: Der mittlere Wert aller Daten entspricht dem Median. Achtung: Bei einer geraden Anzahl von Daten muss der Mittelwert der beiden inneren Werte berechnet werden. Beispiel: Daten: 2,3,6,7 Median: Mittelwert von 3 und 6. (3+6)/2 = 4,5. Im Boxplot ist der Median als eine senkrechte Linie innerhalb der Box zu finden.
- unteres Quartil: Der Median der unteren Hälfte der Datensammlung (unterhalb des Medians) wird als unteres Quartil bezeichnet. Hier beginnt die linke Seite der Box.
- oberes Quartil: Der Median der oberen Hälfte der Datensammlung ( oberhalb des Medians) wird als oberes Quartil bezeichnet. Hier beginnt die rechte Seite der Box.
- Mit den fünf Kenngrößen lässt sich das Boxplot zeichnen.

Häufigkeiten
Bei den Häufigkeiten unterscheidet man zwei Arten.
- Absolute Häufigkeit: Die absolute Häufigkeit entspricht der Anzahl eines Ereignisses in einem Versuch. Also wie oft das gewünschte Ereignis eingetreten ist.
- Beispiel: Eine Münze wird 10 mal geworfen. Die Kopfseite wird 3mal geworfen. Das Ereignis, dass die Kopfseite zu sehen ist, hat die absolute Häufigkeit 3. (=Anzahl des Ereignisses)
- Relative Häufigkeit: Die relative Häufigkeit gibt an, wie oft ein Ereignis in Bezug auf die gesamte Anzahl der Versuche eintritt. Mit anderen Worten, wird hier die absolute Häufigkeit in Verhältnis zum Ganzen gebracht.
- Beispiel: Eine Münze wird 10 mal geworfen. Die Kopfseite wird 3mal geworfen. Das Ereignis, dass die Kopfseite zu sehen ist, hat die relative Häufigkeit: 3/10. (=absolute Häufigkeit/Gesamtanzahl an Versuchen)
- Übungen und Aufgaben dazu

