Umgekehrt proportionale Zuordnung

Alternative Bezeichnungen:
- Anti-proportionaler Dreisatz, Indirekt proportionaler Dreisatz, Umgekehrter Dreisatz
- Anti-proportionale Zuordnung, Indirekt proportionaler Zuordnung, Umgekehrt proportionale Zuordnung
Verwendung:
- Umgekehrt proportionale Zuordnung wird benötigt für Gleichungen in denen sich
  - die eine Größe z.B. verdoppelt
  - während die andere Größe sich halbiert
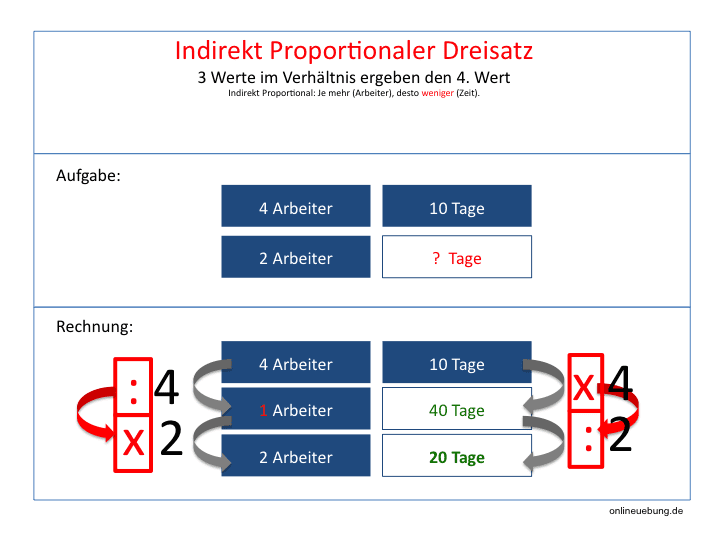
- Beispiel: je mehr Arbeiter an einer Aufgabe arbeiten, desto kürzer die Dauer, um die Aufgabe zu erledigen.
Achtung: 2 Größen sind indirekt proportional, wenn es ein „entgegengesetztes“ Verhalten ist:
- zum 2fachen, 3fachen, 4fachen, … gehört
- die Hälfte, ein Drittel, ein Viertel … der anderen Größe

Beispiel: für ‚proportionalen‘
- Je mehr Maler eingesetzt werden, desto mehr Wände schaffen sie an einem Tag (= proportional)
- Je mehr Personen zum Essen eingeladen sind, desto mehr Brot wird benötigt, bis alle satt sind (= proportional)
- Je mehr Arbeiter benötigt werden, desto höher wird die Rechnung ausfallen. (= proportional)
- Je mehr Pumpen zum Leerpumpen des Kellers eingesetzt werden, desto mehr Wasser können sie in einer Stunde pumpen (= proportional)
- Je mehr Journalisten für eine Zeitung arbeiten, desto mehr Artikel können sie liefern. (= proportional)

Beispiel: für ‚anti-proportionalen‘ Dreisatz:
- Je mehr Maler eingesetzt werden, desto kürzer die Zeit, die sie für eine Wand benötigen. (= umgekehrt proportional)
- Je mehr Personen eingeladen sind, desto kürzer ist die Zeit, die es dauert, bis ein Brot aufgegessen ist (= umgekehrt proportional)
- Je mehr Arbeiter eingesetzt werden, desto kürzer ist die Dauer der Arbeit. (= umgekehrt proportional)
- Je mehr Pumpen eingesetzt werden, desto kürzer die Zeit, um z.B. 100 l Wasser zu pumpen. (= umgekehrt proportional)
- Je mehr Journalisten für eine Zeitung arbeiten, desto kürzer die Zeit, die sie benötigen, um 24 Seiten zu schreiben. (= umgekehrt proportional)

Was ist onlineuebung.de?

onlineuebung.de ist eine kostenlose Lernplattform, für Schülerinnen und Schüler mit Informationen, Links und Onlineübungen.

onlineuebung.de kann man kostenlos abonnieren / folgen und so über Aktualisierungen, neue Inhalte, Aktionen, etc. auf dem Laufenden bleiben.

Weitere Informationen

Direkt Proportional oder Indirekt Proportionaler Dreisatz?

(oder auch ‚Anti-Proportionaler Dreisatz‘ oder ‚Umgekehrt Proportionaler Dreisatz‘)

_{*Sponsored Link.}