Umfangsberechnung üben
Umfangsberechnung üben für verschiedene Figuren: ein Quadrat, ein Rechteck, ein Parallelogramm, eine Raute, ein Trapez, ein Drachenviereck, ein Dreieck und einen Kreis.
- Umfangsberechnung üben für ein Quadrat
- Umfangsberechnung üben für ein Dreieck
- Umfangsberechnung üben für ein Rechteck
- Umfangsberechnung üben für Parallelogramm
- Umfangsberechnung üben für ein Trapez
- Umfangsberechnung üben für eine Raute
- Umfangsberechnung üben für ein Drachenviereck
- Umfangsberechnung üben für einen Kreis


Umfangsberechnung üben
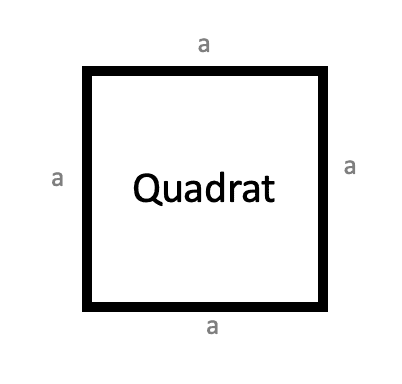
Umfang eines Quadrats berechnen
Leo möchte sein quadratisches Kunstwerk einrahmen.
Das Bild ist 30 cm lang.
Wie viel Meter Rahmen benötigt Leo?
Herr Meyer möchte das Grundstück (6 m x 6 m) einzäunen.
Wie viel Meter Zaun kann er von den 50m wegwerfen?
*Lösungen ganz unten auf dieser Seite.
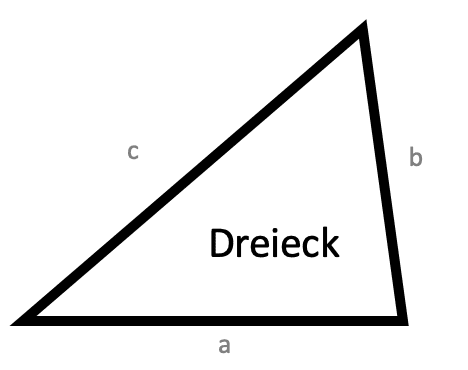
Umfang eines Dreiecks ausrechnen
Martin möchte eine gleichseitige Dreieckschablone ausschneiden.
Die Seitenlänge soll 2 cm betragen.
Berechne den Umfang.
Sophia möchte herausfinden, wie groß der Umfang eines dreieckigen Schildes ist.
Das Schild ist gleichschenklig und 17cm lang.
Die Schenkel betragen jeweils 8cm.
Die Seiten von einer dreieckigen Serviette sind 7,5cm, 4cm und 3,8cm lang.
Berechne den Umfang der Serviette.

*Lösungen ganz unten auf dieser Seite.
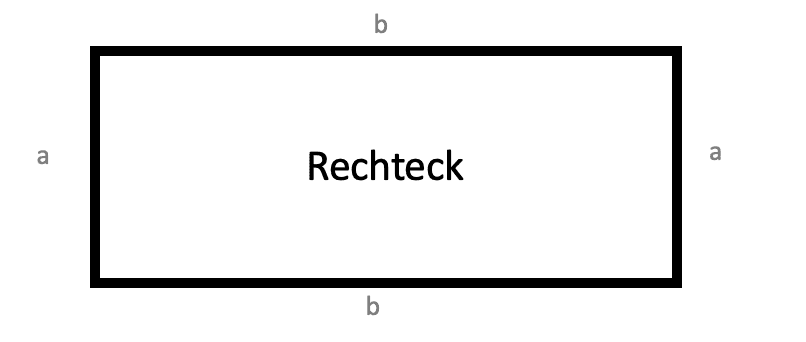
Umfang eines Rechtecks ausrechnen
Frau Meyer möchte ihren rechteckigen Garten einzäunen.
Dieser ist 3 m lang 1,50 m breit.
Wie viel Meter Zaun benötigt sie?
Lisa möchte ihr Kunstwerk einrahmen.
Das Bild ist 0,6 m lang und 4 cm breit.
Wie viel cm Rahmen benötigt sie?

*Lösungen ganz unten auf dieser Seite.
Umfang eines Parallelogramms ausrechnen
Die Seitenlänge eines parallelförmigen Brettspiels beträgt 5 cm und die Breite 20 cm.
Berechne den Umfang.
Ein Schokoriegel hat die Form eines Parallelogramms.
Der Riegel ist 6,2 cm lang und 2,7 cm breit.
Berechne den Umfang.
Eine parallelförmige Decke hat die Länge 2,4 m und die Höhe 1,2 m.
Berechne den Umfang der Decke.


*Lösungen ganz unten auf dieser Seite.
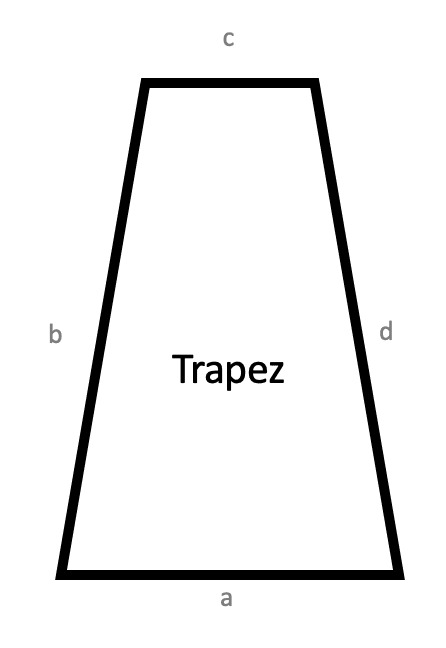
Umfang eines Trapezes ausrechnen
Die vier Seiten eines trapezförmigen Hockers betragen 3,5 m, 5,4 m, 2,8 m und 6,5 m.
Wie groß ist der Umfang?
Ein trapezförmiges Brettstück hat 4 Seiten, die 3,5 m, 1,3 m, 4,6 m und 6,5 m betragen.
Wie groß ist der Umfang?

*Lösungen ganz unten auf dieser Seite.
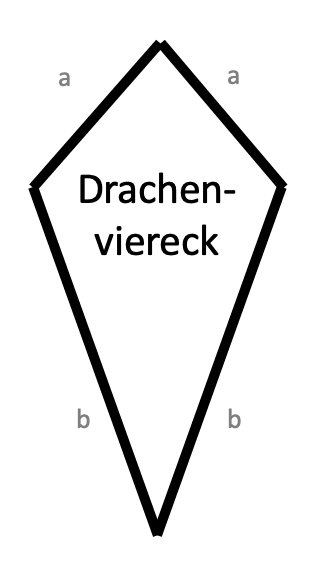
Umfang eines Drachenvierecks ausrechnen
Tom lässt einen Drachen steigen und möchte den Umfang davon wissen.
Die Seitenlängen betragen 3,4 cm und 5,6 cm.
Ein Drachenviereck ist 3,2 m lang und 4,6 m breit.
Wie groß ist der Umfang?
Ein drachenförmiges Tuch ist 140 cm lang und 10 cm.
Bestimme den Umfang.

*Lösungen ganz unten auf dieser Seite.
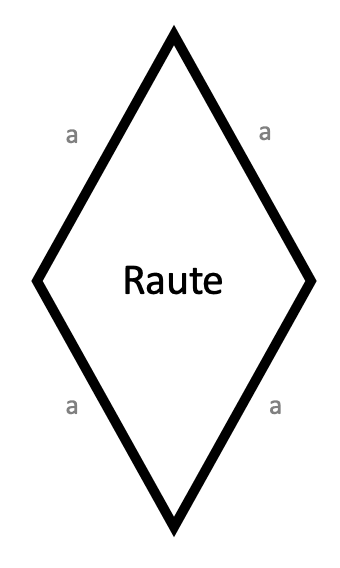
Umfang einer Raute ausrechnen
Maik malt eine Raute und möchte den Umfang davon wissen.
Die Seitenlänge beträgt 6,3 cm.
Ein rautenförmiges Blatt ist 2 cm lang.
Wie groß ist der Umfang?
Eine rautenförmiger Stein ist 90 cm lang.
Bestimme den Umfang.

*Lösungen ganz unten auf dieser Seite.
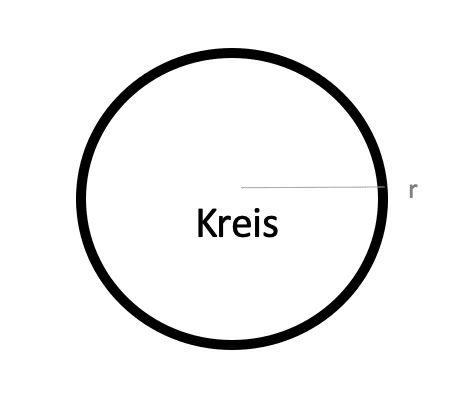
Umfang eines Kreises ausrechnen
Sarah läuft 4 Runden und die Laufbahn ist kreisförmig.
Wie viele Meter ist Sarah gelaufen, wenn der Radius 5 m beträgt?
Runde 1 Stelle nach dem Komma.
Thomas hat einen kreisförmigen Vorgarten.
Er will den Garten mit Steinen umranden.
Ein Stein ist 50 dm lang.
Wie viele Steine braucht Thomas, wenn der Radius vom 6m beträgt?
Runde 1 Stelle nach dem Komma.
Tim möchte den Rand des Kuchens mit einem Radius von 16 cm mit Schokoraspeln bestreuen.
Wie viele cm sind mit Schokoraspeln bedeckt?
Runde 1 Stelle nach dem Komma.

*Lösungen ganz unten auf dieser Seite.
Lösungen zu den Aufgaben
Umfangsberechnung üben
Quadrat
- Aufgabe: Leo möchte sein quadratisches Kunstwerk einrahmen. Das Bild ist 30 cm lang. Wie viel Meter Rahmen benötigt Leo?
- a=30cm=0,3m
- U=4*a= 4*0,3m=1,2 m
- Aufgabe: Herr Meyer möchte das Grundstück (6 m x 6 m) einzäunen. Wie viel Meter Zaun kann er von den 50m wegwerfen?
- a=6m
- U=4*a=4*6m=24m
- 50m-24m=26m
Dreieck
- Aufgabe: Martin möchte eine gleichseitige Dreieckschablone ausschneiden. Die Seitenlänge soll 2 cm betragen. Berechne den Umfang.
- a=b=c=2cm
- U=a+b+c=2cm+2cm+2cm=6cm
- Aufgabe: Sophia möchte herausfinden, wie groß der Umfang eines dreieckigen Schildes ist. Das Schild ist gleichschenklig und 17cm lang. Die Schenkel betragen jeweils 8cm.
- a=17cm b=8cm c=8cm
- U=a+b+c=17cm+8cm+8cm=33cm
- Aufgabe: Die Seiten von einer dreieckigen Serviette sind 7,5cm, 4cm und 3,8cm lang. Berechne den Umfang der Serviette.
- a=7,5cm b=4cm und c=3,8cm
- U=a+b+c=7,5cm+4cm+3,8cm=15,3cm
Rechteck
- Aufgabe: Frau Meyer möchte ihren rechteckigen Garten einzäunen. Dieser ist 3 m lang, 1,50 m breit. Wie viel Meter Zaun benötigt sie?
- a=3m und b=1,50m
- U=2*a+2*b= 2*3m+2*1,50m=9m
- Aufgabe: Lisa möchte ihr Kunstwerk einrahmen. Das Bild ist 0,6 m lang und 4 cm breit. Wie viel cm Rahmen benötigt sie?
- a=0,6m=60cm und b=4cm
- U=2*a+2*b=2*60cm+2*4cm=128cm
Parallelogramm
- Aufgabe: Die Seitenlänge eines parallelförmigen Brettspiels beträgt 5cm und die Breite 20cm. Berechne den Umfang.
- a=5cm und b=20cm
- U=2*a+2*b=2*5cm+2*20cm=50cm
- Aufgabe: Ein Schokoriegel hat die Form eines Parallelogramms. Der Riegel ist 6,2cm lang und 2,7cm breit. Berechne den Umfang.
- a=6,2cm und b=2,7cm
- U=2*a+2*b=2*6,2cm+2*2,7cm=17,8cm
- Aufgabe: Eine parallelförmige Decke hat die Länge 2,4m und die Höhe 1,2m. Berechne den Umfang der Decke.
- a=2,4m und b=1,2m
- U=2*a+2*b=2*2,4m+2*1,2m=7,2m
Trapez
- Aufgabe: Die vier Seiten eines trapezförmigen Hockers betragen 3,5m, 5,4m, 2,8m und 6,5m. Wie groß ist der Umfang?
- a=3,5m, b=5,4m, c=2,8m und d=6,5m
- U=a+b+c+d=3,5m+5,4m+2,8m+6,5m=18,2m
- Aufgabe: Ein trapezförmiges Brettstück hat 4 Seiten, die 3,5m, 1,3m, 4,6m und 6,5m betragen. Wie groß ist der Umfang?
- a=3,5m, b=1,3m c=4,6m und d=6,5m
- U=a+b+c+d=3,5m+1,3m+4,6m+6,5m=15,9m
Drachenviereck
- Aufgabe: Tom lässt einen Drachen steigen und möchte den Umfang davon wissen. Die Seitenlängen betragen 3,4 cm und 5,6 cm.
- a=3,4cm und b=5,6cm
- U = 2*a + 2*b = 2*3,4cm + 2*5,6cm = 18cm
- Aufgabe: Ein Drachenviereck ist 3,2m lang und 4,6m breit. Wie groß ist der Umfang?
- a=3,2m und b=4,6m
- U= 2*a+2*b=2*3,2m+2*4,6m=15,6m
- Aufgabe: Ein drachenförmiges Tuch ist 140cm lang und 10cm. Bestimme den Umfang.
- a=140cm und b=10cm
- U= 2*a+2*b=2*140cm+2*10cm=300cm
Raute
- Aufgabe: Maik malt eine Raute und möchte den Umfang davon wissen. Die Seitenlänge beträgt 6,3 cm.
- a=6,3cm
- U=4*a=4*6,3cm=25,2cm
- Aufgabe: Ein rautenförmiges Blatt ist 2cm lang. Wie groß ist der Umfang?
- a=2cm
- U=4*a=4*2cm=8cm
- Aufgabe: Ein rautenförmiger Stein ist 90cm lang. Bestimme den Umfang.
- a=90cm
- U=4*a=4*90cm=360cm
Kreis
- Aufgabe: Sarah läuft 4 Runden und die Laufbahn ist kreisförmig. Wie viele Meter ist Sarah gelaufen, wenn der Radius 5 m beträgt? Runde 1 Stelle nach dem Komma.
- r=5cm
- U= π*2*r= π*2*5m=10π m≈31,4m
- 31,4 * 4 = 125,6 m
- Aufgabe: Thomas hat einen kreisförmigen Vorgarten. Er will den Garten mit Steinen umranden. Ein Stein ist 50 dm lang. Wie viele Steine braucht Thomas, wenn der Radius vom Garten 6 m beträgt? Runde 1 Stelle nach dem Komma.
- r=6m
- U= π*2*r= π*2*6m=12π m≈37,7m
- Länge vom Stein: 50dm=5m
- 37,7m/5=7,54 Steine≈8 Steine
- Aufgabe: Tim möchte den Rand des Kuchens mit einem Radius von 16 cm mit Schokoraspeln bestreuen. Wie viele cm sind mit Schokoraspeln bedeckt? Runde 1 Stelle nach dem Komma.
- r=16cm
- U= π*2*r= π*2*16cm=32π cm≈100,5cm

