Flächenberechnung üben
Flächenberechnung üben für verschiedene Figuren: ein Quadrat, ein Rechteck, ein Parallelogramm, eine Raute, ein Trapez, ein Drachenviereck, ein Dreieck und einen Kreis.

Flächenberechnung üben
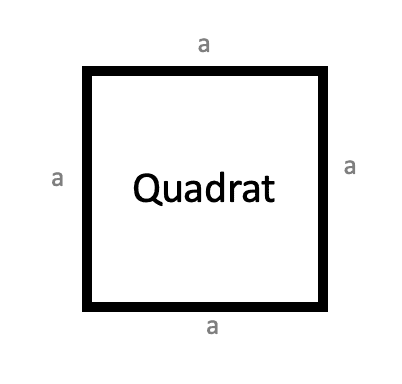
Fläche eines Quadrates berechnen
Kim möchte ihr Kissen (8cm x 8cm) mit Pink bemalen.
Welche Fläche entspricht dies in cm^2?
Frau Müller möchte ihren quadratischen Garten mit Blumenerde füllen.
Der Garten ist 4,5 m lang.
Wie viel kg Blumenerde braucht sie, wenn pro m^2 jeweils 0,5 kg Blumenerde benötigt wird?
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
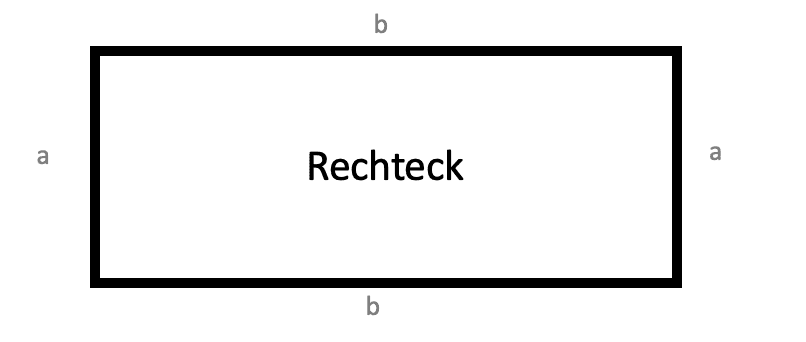
Fläche eines Rechtecks berechnen
Sarah möchte ihr Tisch bedecken.
Der Tisch ist 150 cm lang und 60 cm breit.
Wie viel dm^2 Tuch benötigt sie?
Finn möchte seine Zimmerwand (2 m x 35 dm) mit blauer Farbe anstreichen.
Wie viel Farbe braucht er, wenn pro m^2 200 ml Farbe benötigt wird?
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
Fläche eines Parallelogramms berechnen
Klaus malt ein Parallelogramm und möchte die Flächen wissen.
Die Seite ist 6 cm lang und die Höhe beträgt 2,5 cm.
Ein Brettspiel hat die Form eines Parallelogramms.
Die Höhe beträgt 4 cm und die Seite 23 cm. Bestimme davon die Fläche.
Ein moderner parallelförmiger Teppich hat die Länge 0,63 m und die Höhe 0,9 m.
Berechne die Fläche des Teppichs in dm^2.

*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
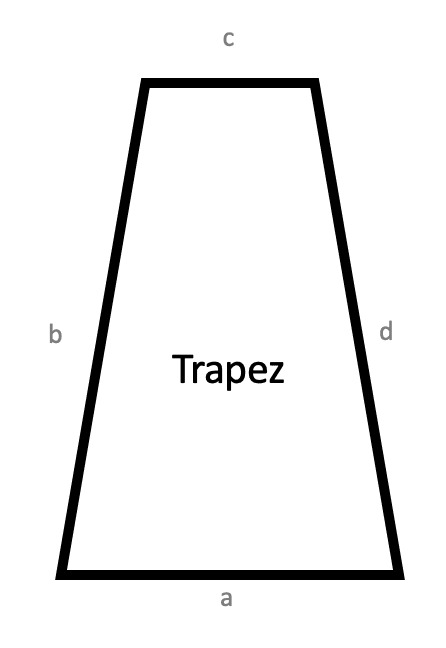
Fläche eines Trapezes berechnen
Jan zeichnet ein Trapez auf einem Papier und möchte die Fläche bestimmen.
Die Seitenlängen betragen 6 dm und 4 dm und die Höhe 7 dm.
Herr Krause hat ein trapezförmiges Brettstück, welches 0,7 m und 0,3 m lang ist.
Die Höhe beträgt 0,4 m. Wie groß ist die Fläche.
Ein trapezförmiges Bild hat die Längen 2,6 m und 4,3 m und die Höhe 1,2 m.
Berechne die Fläche des Bildes.
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
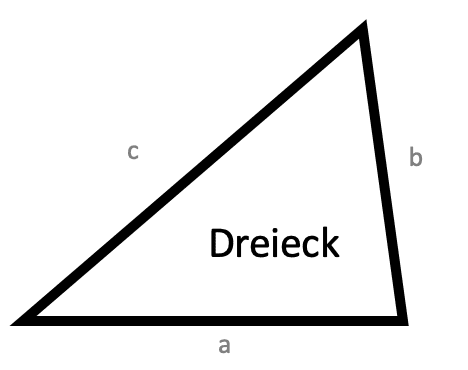
Fläche eines Dreiecks berechnen
Ein dreieckiger Bauklotz ist 5 cm lang und 2 cm hoch.
Berechne die Fläche von 4 dieser Dreiecke.
Ein modernes dreieckiges Fenster ist 5,7 m lang und 760 cm hoch.
Wie viel m^2 Glasfläche wurde hierfür benötigt?
Felix möchte seine dreieckige Leinwand (5 cm lang und 2,5 cm hoch) mit Farbe bemalen.
Wie viel ml Farbe braucht er, wenn pro cm^2 5 ml Farbe benötigt wird?
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
Fläche einer Raute berechnen
Ines malt eine Raute und möchte die Fläche wissen.
Die Diagonalen sind 8 cm lang und 3 cm.
Ein rautenförmiges Tuch hat eine Diagonale, welches 5,8cm lang ist.
Die andere Diagonale beträgt 2,4cm.
Berechne die Fläche.
Eine rautenförmige Platte hat 2 Diagonalen.
Die eine beträgt 1,66cm, die andere 0,02m.
Berechne die Fläche der Platte in cm^2.
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
Fläche eines Drachenvierecks berechnen
Mario lässt einen Drachen steigen und möchte die Fläche wissen.
Die Diagonalen betragen 4,3 m und 5,1 m.
Ein Drachenviereck hat 2 Diagonalen.
Die eine ist 2,3 cm lang und die andere ist 9,3 m breit.
Wie groß ist die Fläche in cm^2?
Ein drachenförmiges Tuch ist 470 cm lang und 37 cm.
Bestimme die Fläche.
*Lösungen ganz unten auf dieser Seite.
Flächenberechnung üben
Fläche eines Kreises berechnen
Max möchte einen kreisförmigen Teig formen.
Wie viel Fläche vom Teig entspricht dies in cm^2, wenn der Radius 10 cm beträgt.
Runde 1 Stelle nach dem Komma.
Frau Meier hat eine Wanduhr.
Der Radius beträgt 12 cm, bestimme die Fläche der Uhr in cm^2.
Runde 1 Stelle nach dem Komma.
*Lösungen ganz unten auf dieser Seite.
Lösungen zur Übung
Flächenberechnung üben
Quadrat
- Aufgabe: Kim möchte ihr Kissen (8cm x 8cm) mit Pink bemalen. Welche Fläche entspricht dies in cm2?
- a=8 cm
- A=a2=(8cm)2=64cm2
- Aufgabe: Frau Müller möchte ihren quadratischen Garten mit Blumenerde füllen. Der Garten ist 4,5 m lang. Wie viel kg Blumenerde braucht sie, wenn pro m 2 0,5 kg Blumenerde benötigt wird?
- a = 4,5m
- A = a2 = (4,5m)2 = 20,25m2
- 20,25m2 * 0,5kg = 10,125 kg
Rechteck
- Aufgabe: Aufgabe: Sarah möchte ihr Tisch bedecken. Der Tisch ist 150 cm lang und 60 cm breit. Wie viel dm2 Tuch benötigt sie?
- a = 150cm und b = 60cm
- A = a*b = 150cm*60cm = 9000cm2 = 90dm2
- Aufgabe: Finn möchte seine Zimmerwand (2 m x 35 dm) mit blauer Farbe anstreichen. Wie viel Farbe braucht er, wenn pro m2 200 ml Farbe benötigt wird?
- a = 2m und b = 35 dm = 3,5m
- A = a*b = 2m*3,5m = 7m2
- 7m2 * 200ml = 1400ml
Parallelogramm
- Aufgabe: Klaus malt ein Parallelogramm und möchte die Fläche wissen. Die Seite ist 6cm lang und die Höhe beträgt 2,5cm.
- a = 6cm und h = 2,5cm
- A = a*h = 6cm*2,5cm = 15cm2
- Aufgabe: Ein Brettspiel hat die Form eines Parallelogramms. Die Höhe beträgt 4cm und die Seite 23cm. Bestimme die Fläche.
- a = 23cm und h = 4cm
- A = a*h = 23cm * 4cm = 92cm2
- Aufgabe: Ein moderner parallelförmiger Teppich hat die Länge 0,63m und die Höhe 0,9m. Berechne die Fläche des Teppichs in dm2.
- a = 0,63m und h = 0,9m
- A = a*h = 0,63m*0,9m = 0,567m2 = 56,7dm2
Trapez
- Aufgabe: Jan zeichnet ein Trapez auf einem Papier und möchte die Fläche bestimmen. Die Seitenlängen betragen 6dm und 4dm und die Höhe 7dm.
- a = 6dm, c = 4dm und h = 7dm
- a = 0,5 * (a+c) * h = 0,5 *(6dm+4dm) * 7dm = 35dm2
- Aufgabe: Herr Krause hat ein trapezförmiges Brettstück, welches 0,7m und 0,3m lang ist. Die Höhe beträgt 0,4m. Wie groß ist die Fläche.
- a = 0,7m, c=0,3m und h=0,4m
- a = 0,5 * (a+c) * h = 0,5 * (0,7m+0,3m) * 0,4m = 0,2m2
- Aufgabe: Ein trapezförmiges Bild hat die Längen 2,6m und 4,3m und die Höhe 1,2m. Berechne die Fläche des Bildes.
- a = 2,6m, c = 4,3m und h = 1,2m
- a =0,5 * (a+c) * h = 0,5*(2,6m + 4,3m) * 1,2m = 4,14m2
Dreieck
- Aufgabe: Ein dreieckiger Bauklotz ist 5 cm lang und 2 cm hoch. Berechne die Fläche von 4 dieser Dreiecke.
- a = 5cm und h = 2cm
- a = 0,5 * a * h = 0,5*5cm*2cm = 5cm2
- 4*5cm2 = 20cm2
- Aufgabe: Ein modernes dreieckiges Fenster ist 5,7m lang und 760cm hoch. Wie viel m2 Glasfläche wurde hierfür benötigt?
- a = 5,7m und h = 760cm = 7,6m
- a = 0,5 * a * h = 0,5*5,7m*7,6m = 21,66m2
- Aufgabe: Felix möchte seine dreieckige Leinwand (5cm lang und 2,5cm hoch) mit Farbe bemalen. Wie viel ml Farbe braucht er, wenn pro cm2 5ml Farbe benötigt wird?
- a = 5cm und h = 2,5cm
- a = 0,5 * a * h = 0,5*5cm*2,5cm = 6,25cm2
- 6,25cm2 * 5ml = 31,25ml
Raute
- Aufgabe: Ines malt eine Raute und möchte die Fläche davon wissen. Die Diagonalen sind 8 cm lang und 3 cm.
- e = 8cm und f = 3cm
- a = 0,5 * e * f = 0,5*8cm*3cm=12cm2
- Aufgabe: Ein rautenförmiges Tuch hat eine Diagonale, welches 5,8cm lang ist. Die andere Diagonale beträgt 2,4cm. Berechne die Fläche.
- e = 5,8cm und f = 2,4cm
- a = 0,5 * e * f =0,5*5,8cm*2,4cm = 6,96cm2
- Aufgabe: Eine rautenförmige Platte hat 2 Diagonalen. Die eine beträgt 1,66cm, die andere 0,02m. Berechne die Fläche der Platte in cm2.
- e =1,66cm und f = 0,02m = 2cm
- a = 0,5 * e * f = 0,5*1,66cm*2cm = 1,66cm2
Drachenviereck
- Aufgabe: Mario lässt einen Drachen steigen und möchte die Fläche wissen. Die Diagonalen betragen 4,3 m und 5,1 m.
- e = 4,3m und f = 5,1m
- a = 0,5 * e * f = 0,5*4,3m*5,1m = 10,965m2
- Aufgabe: Ein Drachenviereck hat 2 Diagonalen. Die eine ist 2,3cm lang und die andere ist 9,3m breit. Wie groß ist die Fläche in cm2?
- e = 2,3cm und f = 9,3m = 930cm
- a = 0,5 * e * f =0,5*2,3cm*930cm = 1069,5cm2
- Aufgabe: Ein drachenförmiges Tuch ist 470cm lang und 37cm. Bestimme die Fläche.
- e = 470cm und f = 37cm
- a = 0,5 * e * f =0,5*470cm*37cm = 8695cm2
Kreis
- Aufgabe: Max möchte einen kreisförmigen Teig formen. Wie viel Fläche vom Teig entspricht dies in cm2, wenn der Radius 10 cm beträgt. Runde 1 Stelle nach dem Komma.
- r = 10cm
- a = π * r2 = π*(10cm)2 = 100 π cm2 ≈ 314,2cm2
- Aufgabe: Frau Meier hat eine Wanduhr. Der Radius beträgt 12 cm, bestimme die Fläche der Uhr in cm2. Runde 1 Stelle nach dem Komma.
- r = 12cm
- a = π * r2 = π* (12cm)2 = 144 π cm2 ≈ 452,4cm2
