Graphen zeichnen und beschreiben

Graphen zeichnen und beschreiben
Graphen lesen und erkennen: Als Grundlage in Mathematik ist das Thema ‚Mathematik: Graphen lesen, erkennen, üben und verstehen‘ wichtig, um darauf aufbauend die ‚Linearen Funktionen‘ zu verstehen, mit Variablen zu rechnen, proportionale und umgekehrt / indirekt / anti-proportionale Zuordnungen und und und und und und und ….
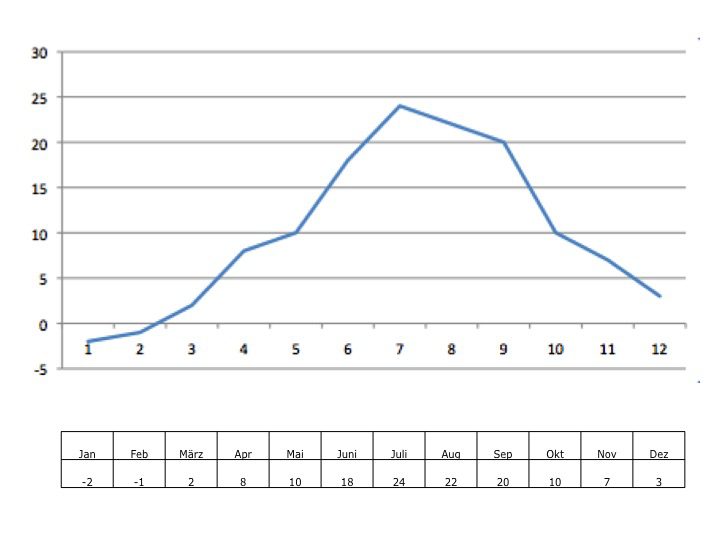
Graphen zeichnen
Um einen Graphen zu zeichnen, geht man wie folgt vor:
-
- Wertetabelle aus den x und y Werten erstellen (1. Spalte x-Werte, 2. Spalte y-Werte) d.h. zu bestimmten x-Werten werden die zugehörigen y-Werte ausgerechnet.
-
- Die Wertepaare werden im Koordinatensystem als Punkte eingetragen (Achtung: zuerst x, dann y: (x/y))
-
- Die Punkte werden miteinander verbunden.
Tipp: Wenn es sich um eine lineare Funktion handelt, reicht es, nur zwei Punkte auszurechnen und diese miteinander zu verbinden.

Graphen beschreiben
Es gibt viele Charakteristika, anhand derer man Graphen beschreiben kann.
-
- Steigung:
-
- steil ansteigende Steigung (m > 0)
-
- stark abfallende Steigung (m < 0)
-
- linearer Anstieg / lineare Abnahme (die positive / negative Steigung der linearen Funktion ist an allen Punkten gleich groß)
-
- exponentieller Anstieg (zuerst sehr stark ansteigen, dann nur wenig ansteigen),
-
- exponentielle Abnahme (zuerst sehr stark abnehmen, dann nur wenig abnehmen)
-
- Steigung:
-
- Nullstelle: Der Punkt, an dem der Graph die x-Achse berührt. (Beispiel: In einem Zeit-Geschwindigkeits-Diagramm oder auch t-v-Diagramm genannt gibt er den Zeitpunkt an, an dem die Geschwindigkeit v=0 ist).
-
- Maximum / Minimum: Der Hochpunkt bzw. der Tiefpunkt (Beispiel: In einem t-v-Diagramm gibt er die maximale oder minimale Geschwindigkeit an)
-
- Schnittpunkt mit y-Achse: Der Punkt, an dem der Graph die y-Achse berührt. (Beispiel: In einem t-v-Diagramm gibt er die Anfangsgeschwindigkeit zum Zeitpunkt t=0 an).

Symmetrie bei Graphen
Man unterscheidet bei Graphen zwischen
-
- Asymmetrie (keine Symmetrie),
-
- Punktsymmetrie (drehsymmetrisch zu einem Punkt, meist der Ursprung P(0/0)) und
-
- Achsensymmetrie (spiegelsymmetrisch zur y-Achse).

Graphen zeichnen und beschreiben
-
- Online-Übung (Zuordnung und Graphen)
- Online-Übung (Graphen erkennen: proportional, linear, anti-proportional) – mit Onlineüberprüfung!!! Klick auf ‚Kontrolle‘
- Online-Übung (Graphen erkennen: proportional, linear, anti-proportional) – mit Onlineüberprüfung!!! Klick auf ‚Kontrolle‘
- Online-Übung: Graphen nach Vorgaben zeichnen (ziehen) – mit Onlinekontrolle
Lineare Zuordnungen
- Interaktive Onlineübung: Geradengleichung ablesen, ….
