Was ist Dividieren? - Schriftliches Dividieren
Was ist Dividieren? – Schriftliches Dividieren mit und ohne Rest. Hier findest du einfach verständliche Erklärungen und Herleitungen.
Einfache Erklärung
„Dividieren“ kommt von „dividere“ = „teilen. Beim Dividieren geht es also ums Teilen.
- Definition: Dividieren heißt Teilen.
- Beispiel:
- Peter und Michael bestellen eine Pizza und teilen sie.
- Jeder erhält die Hälfte.
- Man rechnet: 1 : 2 = 1/2
- Begriffe der Division
- Dividend = ‚die Pizza‘
- Divisor = ‚Peter und Michael‘ = 2
- Quotient = das Ergebnis = 1/2
- Symbole der Division
- Beispiele
- 12 / 4 = 3
- 9 : 3 = 3
- 25 : 5 = 5
Schriftliches Dividieren
Bei größeren Zahlen dividiert man schriftlich (oder mit dem Taschenrechner). Dabei wird der Dividend, das zu teilende Objekt, von links nach rechts durch den Divisor, die Zahl, durch die geteilt wird, geteilt.
Beispielaufgabe: 51 : 3
- Schritt: vom Dividend (hier 51) zunächst die 5 durch den Divisor (hier 3) teilen. Ergebnis 1.
2. Schritt: die 3 wird von der 5 abgezogen: es bleiben 2.
Dann wird die nächste Zahl des Dividenden ’nach unten‘ gezogen,
und durch 3 geteilt. Ergebnis 7.
Da die 51 nun quasi verteilt / geteilt wurde – und kein Rest bleibt – ist das Ergebnis: 17.
Übungen dazu
Dividieren mit Rest
Würde die Aufgabe lauten: 52 : 3, wäre die Rechnung wie folgt:
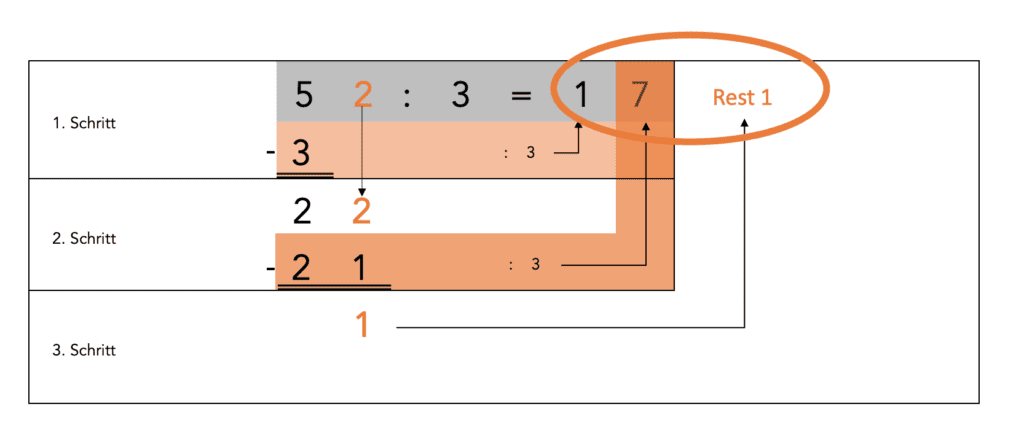
Es bleibt am Ende 1 übrig. 1 ist aber nicht mehr durch 3 teilbar. Daher sagt man: das Ergebnis (der Quotient) ist 17 – Rest 1.
Übungen dazu
Dividieren, wenn der Quotient < 0 ist
Wenn der Divisor größer als der Dividend ist, ist das Ergebnis kleiner 0.
Beispielaufgabe: 2 : 5 = ?
- Schritt: Den Dividend (2) durch den Divisor (5) teilen. Da der Divisor größer ist als der Dividend, ist das Ergebnis zunächst 0.
- Schritt: Die 0 wird von der 2 (Dividend) abgezogen, bleibt die 2 übrig. Jetzt gibt es keine weitere Zahl, die ’nach unten‘ gezogen werden kann: Trick: man zieht sich quasi eine 0 herunter, d.h. jetzt steht dort eine 20.
- Schritt: Im Ergebnis schreibt man ein Komma nach der 0.
- Schritt: Die 20 wird durch die 5 geteilt: ergibt 4. Als Ergebnis kommt 0,4 raus, eine Dezimalzahl.
Hinweis: Es könnte auch der Fall sein, dass das Ergebnis keine endliche (abbrechende) Zahl ist, sondern unendlich viele Nachkommastellen hat.
Übungen dazu
- Dividieren, wenn der Quotient kleiner 0 ist – einfache Aufgaben
Arten von Dezimalzahlen
- Abbrechende Dezimalzahlen: Abbrechende Dezimalzahlen haben endlich viele Nachkommazahlen, d.h. n Nachkommastellen. Zum Beispiel: 0,25 oder 0,8675.
- Nicht-abbrechend Dezimalzahlen: Nicht abbrechende Dezimalzahlen haben unendlich viele Nachkommastellen. Zum Beispiel: 0,53268….
- Periodische Dezimalzahlen: Sonderfall der nicht-abbrechenden Dezimalzahlen. Die Nachkommastellen wiederholen sich bei periodische Dezimalzahlen! Zum Beispiel: 0,333333 … , dies kürzt man mit einem Strich über den Zahlen, die wiederholt werden ab. Beispiel: 0,33333 … oder 0,161616 schreibt man auch:
