Winkel berechnen
Winkel berechnen – Winkel und Winkelarten für den Matheunterricht
Winkel und Winkelarten
- Nullwinkel: ein Nullwinkel hat 0 Grad. Ein Nullwinkel sieht aus wie eine Gerade, weil die beiden Winkel aufeinander liegen.
- Spitzer Winkel: ein spitzer Winkel hat zwischen 0 und 90 Grad.
- Rechter Winkel: ein rechter Winkel hat 90 Grad.
- Stumpfer Winkel: ein stumpfer Winkel hat zwischen 90 und 180 Grad.
- Gestreckter Winkel: ein gestreckter Winkel hat 180 Grad und ist damit auch eine Gerade.
- Überstumpfer Winkel: ein überstumpfer Winkel hat 180 – 360 Grad.
- Vollwinkel: ein Vollwinkel hat 360 Grad. Ein Vollwinkel sieht auch aus wie eine Gerade, weil auch hier die Schenkel aufeinander liegen.
Wo Winkel in der Praxis vorkommen und wie man sie berechnet
Nullwinkel: wenn bei einem Zollstock die Stäbe aufeinander liegen, der Zollstock also zugeklappt ist, haben die Stäbe einen Nullwinkel (0o).
Ein Nullwinkel hat immer 0o und muss daher nicht berechnet werden.

Spitzer Winkel: ein Stück Pizza hat einen spitzen Winkel (< 90o).
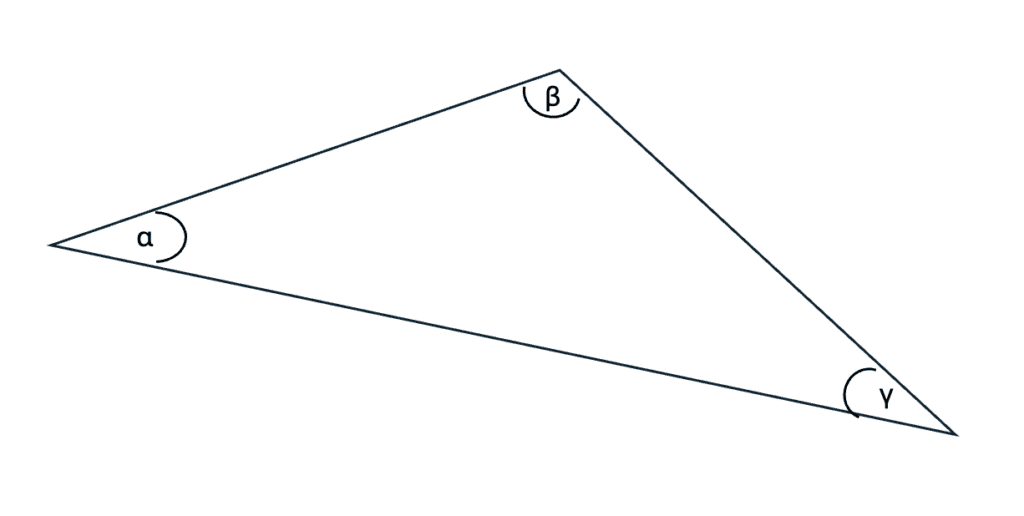
Zur Berechnung eines spitzen Winkels nutzt man die Logik, dass die Summe der Winkel in einem Dreieck immer 180° beträgt. D.h.
- α + β + γ = 180
oder auch
- α = 180 −β – γ

Rechter Winkel: ein Fenster hat normalerweise rechte Winkel (90o).
Ein Rechter Winkel hat immer 90o und muss daher nicht berechnet werden.

Stumpfer Winkel: Die Zeiger der Uhr bilden einen sogenannten Stumpfen-Winkel, wenn es beispielsweise 4 Uhr ist (> 90o).
Zur Berechnung eines Stumpfen Winkels nutzt man die Logik, dass die Summe der Winkel in einem Dreieck immer 180° beträgt. D.h.
- α + β + γ = 180
oder auch
- α = 180 −β – γ
Gestreckter Winkel: Beim Spagat sind die Beine im Gestreckten Winkel (180o).
Ein Gestreckter Winkel hat immer 180o und muss daher nicht berechnet werden.

Eine Gerade ist auch ein Gestreckter Winkel (180o).

Auch eine Kehrtwende hat einen Gestreckten Winkel (90o + 90o = 180o).
Eine Kehrtwende hat immer 180o und muss daher nicht berechnet werden.

Überstumpfer Winkel: In der Relaxposition beim Yoga haben die Arme einen Überstumpfen Winkel (180-360o).
Ein überstumpfer Winkel kann in Bezug auf einen vollständigen Kreis (360°) berechnet werden. Wenn der kleinere Winkel α bekannt ist, dann ist der überstumpfe Winkel β=360∘−α.

Vollwinkel: Wenn sich die Welt einmal pro Tag um die eigene Achse dreht, sind das 360o = ein Vollwinkel.
Ein Vollwinkel hat immer 360o und muss daher nicht berechnet werden!
Betrachtet man den Vollwinkel im Ergebnis, sieht der Vollwinkel auch aus wie eine Gerade (siehe Bild rechts).

Winkel in der Übersicht
| Grad | Genaue Definition | Bezeichnung |
| 0 Grad | α = 00 | Nullwinkel |
| zwischen 0 und 90 Grad | 00 < α < 900 | Spitzer Winkel |
| 90 Grad | α = 900 | Rechter Winkel |
| zwischen 90 und 180 Grad | 900 < α < 1800 | Stumpfer Winkel |
| 180 Grad | α = 1800 | Gestreckter Winkel |
| zwischen 180 und 360 Grad | 1800 < α < 3600 | Überstumpfer Winkel |
| 360 Grad | α = 3600 | Vollwinkel |
Übungen zu den Winkelarten
- Fragen zu Winkeln beantworten
- Tool: Winkel zeichnen (Schenkel auf dem Bildschirm verschieben)
- Spiel: Winkel kennen
- Spiel: Winkel kennen
- Spiel: Winkel schätzen
- Begriffe (Kreuzworträtsel zu Winkeln)
Diverse weiterführende Links:
- Video: Wozu werden Winkel in der Praxis benötigt?
Auch interessant
