Symmetrie lernen
Symmetrie bedeutet Ebenmaß, Gleichmaß oder auch Spiegelbildlichkeit. Heißt also, es geht um spiegelgleiche Objekte.
Symmetrie
In der Mathematik und Geometrie spricht man über Symmetrie, wenn ein Objekt (vereinfacht gesagt) auf sich selbst gespiegelt werden kann. Genauer gesagt: auf sich selbst abgebildet werden kann.
Es gibt unterschiedliche Arten:
- Achsensymmetrie: Spiegelung erfolgt über eine Achse.
- Punktsymmetrie: Spiegelung erfolgt über einen Punkt.
- Rotationssymmetrie: Spiegelung durch Drehung.
- Asymmetrie: wenn etwas nicht gleich ist, wenn man es spiegelt. (Asymmetrie ist das Gegenteil von Symmetrie)
Achsensymmetrie / Spiegelsymmetrie
- Definition: wenn man eine Figur in zwei Teile teilen kann, die
- wie gespiegelt aussehen,
- mindestens eine Symmetrieachse (Faltkante) haben,
- exakt deckungsgleiche Teile ergeben.
Symmetrie-Achse
- Definition: die Symmetrieachse ist die Spiegelachse, an der man ein Objekt spiegeln kann, um es „auf sich selbst abzubilden“
- Die Symmetrieachse kann senkrecht, waagrecht oder diagonal verlaufen.
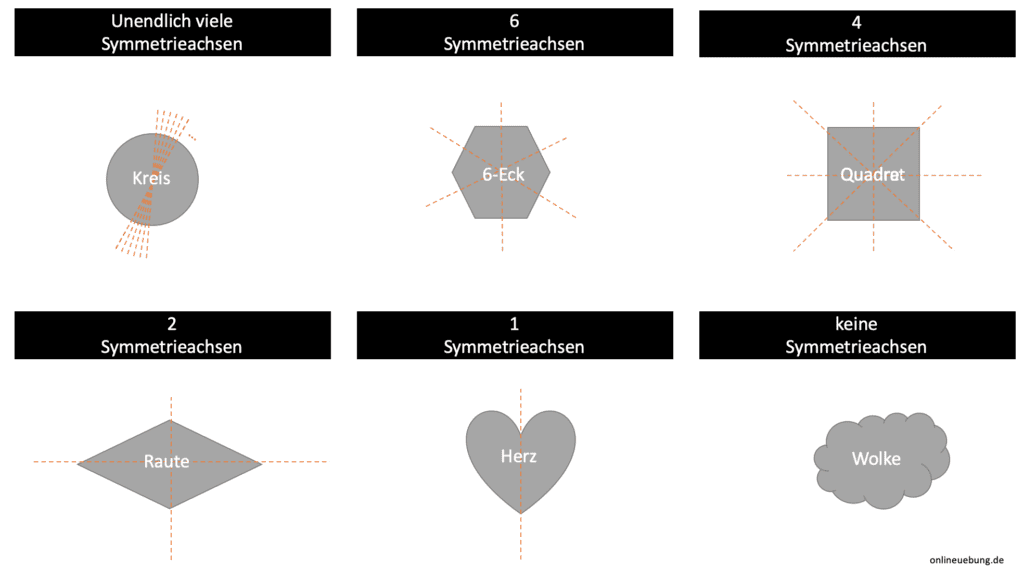
- Unendliche viele Symmetrieachsen haben:
- Kreis
- Gerade (da sie unendlich lang ist, ist sie symmetrisch bezüglich jeder zu ihr senkrecht stehenden Achse + der auf ihr selbst liegenden Achse)
- 6 Symmetrie-Achsen hat ein Sechs-Eck
- 4 Symmetrie-Achsen ein Quadrat
- 2 Symmetrie-Achsen
- Buchstaben: H, O, X, I
- Raute
- Rechteck
- 1 Symmetrie-Achse
- Buchstaben: A, C, D, E, M, T, U, V, W, Y, B, K
- Gleichschenkeliges Dreieck
- Trapez
- Herz
Strecken und Geraden
Konstruktion: man erhält eine Gerade oder eine Strecke durch die Verbindung von 2 Punkten mit einer geraden Linie, entlang eines Lineals.
Strecken
- Als Strecken werden bezeichnet:
- gerade Linien
- mit einem Anfangs- und einem Endpunkt.
- Die Endpunkte werden mit AB bezeichnet.
Gerade
- Als Geraden werden bezeichnet:
- Unbegrenzte Strecken.
- Diese werden mit ‚g‘ bezeichnet.
Parallel und Orthogonal
Parallele Geraden und Strecken
- Zwei Strecken oder Geraden sind parallel, wenn sie
- in jedem Punkt denselben Abstand haben
- und sich nie schneiden.
Somit haben parallele Geraden und Strecken immer dieselbe Steigung.
Orthogonale Geraden und Strecken
- Zwei Strecken oder Geraden sind orthogonal,
- wenn sie senkrecht zueinander sind.
- wenn die Geraden einen rechten Winkel zueinander bilden.
Punktsymmetrie
- Definition: eine Figur ist punktsymmetrisch, wenn
- eine Drehung um 180° vorliegt bzw.
- sie an einem Spiegelzentrum/ Spiegelpunkt gespiegelt wird.
- Punktsymmetrische Figuren sind automatisch auch drehsymmetrisch.
- Beispiele: Buchstaben: S, N, Z
Spiegelzentrum/ Spiegelpunkt
- Definition: Das Spiegelzentrum bzw. der Spiegelpunkt ist der Punkt, an dem gespiegelt wird, um die Figur auf sich selbst abzubilden/ zur Deckung zu bringen.
- Gleichzeitig kann das Spiegelzentrum auch als Drehzentrum betrachtet werden, da die Drehung um 180° einer Punktspiegelung entspricht.
Rotationssymmetrie/ Drehsymmetrie
- Definition: eine Figur ist rotationssymmetrisch, wenn
- eine Drehung um einen beliebigen Winkel vorliegt bzw.
- sie an einem Drehzentrum gespiegelt wird.
Drehzentrum
- Definition: Das Drehzentrum ist der Punkt, an dem gedreht wird, um die Figur auf sich selbst abzubilden.
- Bemerkung: Bei einer Drehung um 180° ist das Drehzentrum auch das Spiegelzentrum, da es sich um eine Punktsymmetrie/Punktspiegelung handelt.
Asymmetrie
- Definition: eine Figur ist asymmetrisch, wenn
- weder eine Achsensymmetrie
- noch eine Punktsymmetrie oder Rotationssymmetrie vorliegt.
- Asymmetrische Figuren können NICHT miteinander in Deckung gebracht werden.
Symmetrie: Aufgaben und Übungen
- Quiz Symmetrie
- Quiz: Geometrie
- Quiz: Geometrie
- Ordne zu: Welche Figur hat wie viele Symmetrieachsen?
- Tool: Spiegel die Figur: Dreieck, Viereck, Fünfeck, Sechseck
- Vorgehen bei der Achsspiegelung
- Diverse
- Arbeitsblätter
Weiteres zur Geometrie
- Figuren und Körper
- Berechnungen
- Grundlagen
