Bruchrechnen

Definition Bruchrechnen:

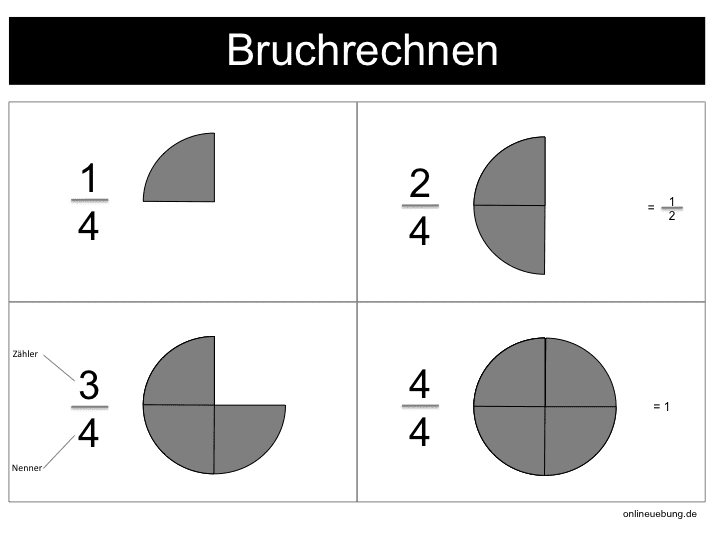
Wie ist ein Bruch aufgebaut?

Brüche haben einen

Zähler: steht über dem Bruchstrich und gibt an, wie viele Anteile von etwas „gezählt“ wurden.
Nenner: steht unter dem Bruchstrich und gibt an, wie viele Teile ein Ganzes hat.

Arbeiten mit Brüchen

Kürzen – Wie kürzt man?
- Definition: beim Kürzen geht es darum, die Zahlen des Bruches möglichst klein zu machen, bis sie teiler-fremd sind. (teiler-fremd = Zähler ist nicht durch den Nenner teilbar und umgekehrt)
- Vorgehen: Zähler und Nenner durch die gleiche Zahl teilen (dividieren)
  - Möchte man einen Bruch so weit wie möglich kürzen,
  - sucht man den ‚größten gemeinsamen Teiler‘ (= ggT) vom Zähler und Nenner
  - dann teilt man Zähler und Nenner mit dem ggT, sodass Zähler und Nenner teiler-fremd sind.
- Übungen: Brüche kürzen

Erweitern
- Definition: beim Erweitern (oder auch gleichnamig machen) werden verschiedenartige Brüche auf den gleichen Nenner gebracht, damit man danach leichter mit ihnen weiter rechnen kann.
- Vorgehen: wenn man zwei Brüche gleichnamig machen möchte,
  - sucht man das ‚Kleinste gemeinsame Vielfache‘ = kgV beider Nenner,
  - dann multipliziert Zähler und Nenner des einen Bruches mit der gleichen Zahl, sodass im Nenner (!) das kgV beider Brüche steht.
  - Dann multipliziert man Zähler und Nenner des anderen Bruches mit der gleichen Zahl (muss nicht die Zahl des ersten Bruches sein), sodass auch hier im Nenner (!) das kgV beider Brüche steht.
- Beispiel:
  - Aufgabe: Mache die Brüche 1/3 und 1/5 gleichnamig.
  - Beide Brüche werden auf den Nenner 15 erweitert.
  - Dazu wird 1/3 mit 5 multipliziert: 1/3 * 5 = 5/15
  - Und 1/5 wird mit 3 multipliziert: 1/5 * 3 = 3/15
  - Beide Brüche haben nun den Nenner ’15‘.
  - Damit sind sie ‚gleichnamig‘.
- Übungen dazu: Brüche erweitern

Addieren
- Voraussetzung: Brüche können nur addiert werden, wenn der Nenner gleich ist
- Vorgehen:
  - Nenner angleichen (siehe oben – ‚Erweitern‘)
  - Zähler + Zähler / Nenner beibehalten
- Übungen dazu: Brüche addieren
Subtrahieren
- Voraussetzung: Brüche können nur subtrahiert werden, wenn der Nenner gleich ist
  Vorgehen:
  - Nenner angleichen
  - Zähler – Zähler / Nenner beibehalten
  - Übungen dazu: Brüche subtrahieren üben
Multiplizieren
- Vorgehen: man multipliziert Brüche, indem man Zähler mal Zähler und Nenner mal Nenner nimmt.
- Übungen dazu: Brüche multiplizieren üben
Dividieren
- Vorgehen: man dividiert Brüche, indem man mit dem Kehrwert multipliziert.
- Kehrwert: Zähler und Nenner werden vertauscht: 3/4 => 4/3
- Übungen dazu: Brüche dividieren üben