Additionsverfahren üben um das Lineare Gleichungssystem mit dem Einsetzungsverfahren, Gleichsetzungsverfahren, Additionsverfahren besser zu verstehen.

Additionsverfahren üben

Berechne mit dem Additionsverfahren und wähle dann die richtige Lösung aus.

Einfache Übungen

^{*Lösungen und Rechenwege ganz unten auf dieser Seite.}

Mittelschwierige Übungen

^{*Lösungen und Rechenwege ganz unten auf dieser Seite.}

Schwierige Übungen

^{*Lösungen und Rechenwege ganz unten auf dieser Seite.}

Erklärungen und Beispiele

• Lineare Gleichungssysteme
• Einsetzungsverfahren
• Gleichsetzungsverfahren
• Additionsverfahren

Weitere Übungen: Additionsverfahren üben

• Einsetzungsverfahren üben
• Gleichsetzungsverfahren üben
• Additionsverfahren üben

---

Viele weitere hilfreiche Infos für den Matheunterricht.

---

Was ist onlineuebung.de? 

onlineuebung.de ist eine kostenlose Lernplattform, für Schülerinnen und Schüler mit Informationen, Links und Onlineübungen.

onlineuebung.de kann man kostenlos abonnieren / folgen und so über Aktualisierungen, neue Inhalte, Aktionen, etc. auf dem Laufenden bleiben.

Lösungen und Rechenwege: Additionsverfahren üben

Einfache Übungen – Additionsverfahren üben

Aufgabe: (1) 5x – 15y = 25 und (2) x – 2y = 20

umformen von x zu -5x:

(2): x-2y  =  20 |*(-5)

<=> -5x + 10y = -100

addieren:

einsetzen in (1): 5x-15*15 = 25

<=> 5x-225 = 25 | + 225

<=> 5x = 250 |/5

<=> x = 50

Aufgabe: (1) x – 2y =  -12 und (2) 9x – 3y =  27

umformen von x zu -9x:

(1): x-2y = -12 |*(-9)

<=> -9x + 18y = 108

addieren:

einsetzen in (1): x-2*9 = -12 

<=> x-18 = -12 | + 18

<=> x = 6

Aufgabe: (1) 3x  +  6y = 12 und (2) x – 3y = 9

umformen von x zu -3x:

(2): x-3y = 9 |*(-3)

<=> -3x + 9y = -27

addieren:

einsetzen in (1): 3x + 6*(-1) = 12

<=> 3x-6 = 12 | + 6

<=> 3x = 18 |/3

<=> x = 6

Aufgabe: (1) 8x = 40y und (2) x = 15 – 10y

umformen von x zu -8x:

(2): x = 15-10y |*(-8)

-8x = -120 + 80y

addieren:

einsetzen in (1): 8x = 40*1

<=> 8x = 40 |/8

<=> x = 5

Aufgabe: (1) 0,5x = 2y + 10 und (2) x = 12y + 4

umformen von x zu 0,5x:

(2): x = 12y + 4 |*(-0,5)

<=> -0,5x = -6y-2

addieren:

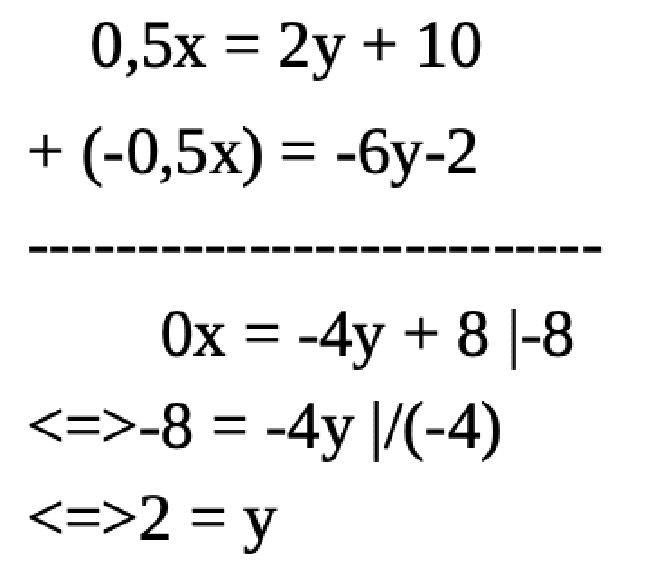
einsetzen in (1): 0,5x = 2*2 + 10 

<=> 0,5x = 14 |/0,5

<=> x = 28

Mittelschwierige Übungen – Additionsverfahren üben

Aufgabe: (1) 8x – 2y = 12 und (2) 4x – 2y = 60

umformen von 4x zu -8x:

(2): 4x – 2y  =  60 |*(-2)

<=> -8x + 4y = -120

addieren:

einsetzen in (1): 8x-2*(-54) = 12

<=> 8x  + 108 = 12 |-108

<=> 8x = -96 |/8

<=> x = -12

Aufgabe: (1) 3x – 4y = 10 und (2) 3x – 2y = 26

umformen von 3x zu -3x:

(1): 3x – 4y = 10 |*(-1)

<=> -3x + 4y = -10

addieren:

einsetzen in (1): 3x – 4*8 = 10

<=> 3x – 32 = 10 |+32

<=> 3x = 42 |/3

<=> x = 14

Aufgabe: (1) 3x + 3y = 12 und (2) x – 4y = 8

umformen von x zu -3x:

(2): x-4y = 8 |*(-3)

<=> -3x+12y = -24

addieren:

einsetzen in (1): 3x+3*(-4/5) = 12

<=> 3x-12/5 = 12 |+12/5

<=> 3x = 72/5 |/3

<=> x = 24/5

Aufgabe: (1) 5x + 10 = 2y und (2) x = 10 – 2y

umformen von x zu -5x:

(2): x = 10-2y |*(-5)

<=> -5x = -50+10y |+50

<=> -5x+50 = 10y

addieren:

einsetzen in (1): 5x+10 = 2*5

<=> 5x+10 = 10 |-10

<=> 5x = 0 |/5

<=> x = 0

Aufgabe: (1) 4y – 4x = 4 und (2) 2y – x = 5

umformen von 2y zu -4y:

(2): 2y-x = 5 |*(-2)

<=> -4y+2x = -10

addieren:

einsetzen in (1): 4y-4*3 = 4 

<=> 4y-12 = 4 |/+12

<=> 4y = 16 |/4

<=> y = 4

Schwierige Übungen – Additionsverfahren üben

Aufgabe: (1) 4x – 3y = 7 und (2) 4x – 2y = 36

umformen von 4x zu -4x:

(2): 4x-2y  =  36 |*(-1)

<=> -4x+2y = -36

addieren:

einsetzen in (1): 4x-3*29 = 7

<=> 4x-87 = 7 | + 87

<=> 4x = 94 |/4

<=> x = 23,5

Aufgabe: (1) -5x – 3y = 5 und (2) -5x – 6y = 35

umformen von -5x zu 5x:

(1): -5x-3y = 5 |*(-1)

<=> 5x + 3y = -5

addieren:

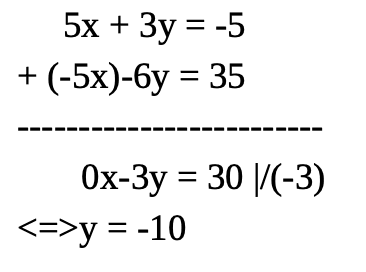
einsetzen in (1): -5x-3*(-10) = 5

<=> -5x + 30 = 5 |-30

<=> -5x = -25 |/(-5)

<=> x = 5

Aufgabe: (1) 2x – 2y = -20 und (2) 2x – 4y = 35

umformen von 2x zu -2x:

(2): 2x-4y = 35 |*(-1)

<=> -2x + 4y = -35

addieren:

einsetzen in (1): 2x-2*(-27,5) = -20

<=> 2x + 55 = -20 |-55

<=> 2x = -75 |/2

<=> x = -37,5

Aufgabe: (1) -4x + 20 = 7y und (2) x = 25 – 2y

umformen von x zu 4x:

(2): x = 25-2y |*4

<=> 4x = 100-8y

addieren:

einsetzen in (1): -4x + 20 = 7*8

<=> -4x + 20 = 560 |-20

<=> -4x = 540 |/(-4)

x = -135

Aufgabe: (1) y – 3x = -10 und (2) -6y – 2x = 16

umformen von y zu 6y:

(1): y-3x = -10 |*6

<=> 6y-18x = -60

addieren:

einsetzen in (1): y-3*2,2 = -10 

<=> y-6,6 = -10 | + 6,6

<=> y = -3,4