Rechengesetze: Kommutativgesetz, Assoziativgesetz, Distributivgesetz

Rechengesetze
- Infografik zu den Rechengesetzen
- Spickzettel zu den Rechengesetzen
Grundlage: Punkt vor Strichrechnung
Kommutativgesetz
Assoziativgesetz
Distributivgesetz
Übungen

Rechengesetze: Kommutativgesetz, Assoziativgesetz, Distributivgesetz

Absolutes ‚Must know‘ der Mathematik: die Rechengesetze. Die Rechengesetze sind soetwas wie das Grundgesetz der Mathematik! Und um diese Grundgesetze kommt keiner herum! Warum? Weil sie in den anderen Themen immer wieder vorkommen, vorausgesetzt und ständig angewendet werden. Entsprechend macht es größten Sinn, die Grundgesetze zu lernen und zu verstehen. Also: lesen, lernen und üben!!!!

Man nennt die Rechengesetze auch:

Kommutativgesetz: Vertauschungsgesetz
Assoziativgesetz: Verbindungsgesetz
Distributivgesetz: Verteilungsgesetz oder auch Klammergesetz, bei dem es ums Ausmultiplizieren und Auflösen von Klammern geht

Infografik Rechengesetze: Kommutativgesetz, Assoziativgesetz, Distributivgesetz

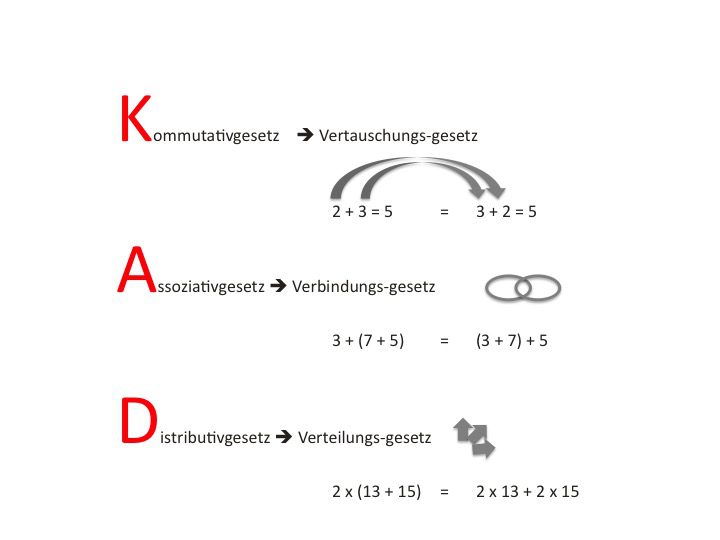
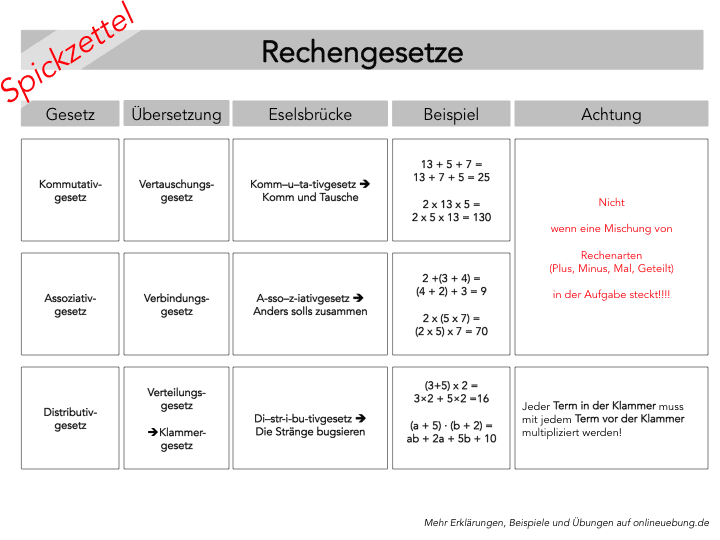
Rechengesetze: Kommutativgesetz, Assoziativgesetz, Distributivgesetz

– Spickzettel –

Zum kostenlosen Download: auf der Übungsseite

Grundlage: Punkt vor Strichrechnung

Für die Rechengesetze gilt immer die Grundregel: Punkt vor Strichrechnung!

Damit kann man alle Gesetze herleiten, erklären und verstehen.

- Anwendung:
  - - Bei Aufgaben, in denen + und – Aufgaben mit • und: gemischt sind
  - - d.h. Aufgaben in denen Addition und Subtraktion mit Multiplikation, Division vorkommen
  - - ggf. auch noch mit Klammern

- Merksatz: Punkt vor Strichrechnung

- Übersetzung: Zuerst müssen die Teile mit • und: gerechnet werden, bevor die Teile mit + und – gerechnet werden.

- Beispiel: 5 + 3 • 2 = 11 (nicht 16)
  - - Richtiger Rechenweg:
      - 5 + (3 • 2) =
      - 5 + 6 = 11

- Übung dazu – 1-
- Übung dazu – 2-

1. Kommutativgesetz

= Vertauschungsgesetz der Addition und Multiplikation

- Kommutativgesetz: Vertauschungsgesetz

- Übersetzung: commutare = vertauschen

- Merksatz Kommutativgesetz / Eselsbrücke: Komm–u–ta-tivgesetz => Komm und Tausche.

- Anwendung: bei Aufgaben mit mehreren Additionen oder Multiplikationen
  - - Einfache Formulierung: wenn die Aufgabe
      - nur Plusaufgaben oder nur Malaufgaben hat;
      - (d.h. nur Strichrechnung oder nur Punktrechnung (einer Art))
      - darf getauscht werden.

- Achtung:
  - - NICHT wenn eine Mischung von Rechenarten in der Aufgabe steckt!!!! D.h.
      - wenn Plus (+) und Minus (-) in der Aufgabe gemischt sind!
      - wenn Plus (+) und Mal (x) in der Aufgabe sind!
  - - NICHT bei Subtraktion oder Division !!!!!!!!!!!!!!!!!!!!!!

- NUR bei reinen Additionen oder Multiplikationen

- Gesetz: es ist egal, welche der Additionen / Multiplikationen zuerst gemacht wird
  - - Beispiel: 13 + 5 + 7 = 13 + 7 + 5 = 25
  - - Beispiel: 2 x 13 x 5 = 2 x 5 x 13 = 130

Achtung, Achtung, Achtung:

- Nicht bei Subtraktion oder Division!

- Auch nicht, wenn Addition und Multiplikation gemischt sind!

Übungen

2. Assoziativgesetz

= Verbindungsgesetz

= Assoziativgesetz der Addition und Multiplikation

- Assoziativgesetz: Verbindungsgesetz,
  - - Es geht ums Ausmultiplizieren und Auflösen von Klammern.

- Übersetzung: Assoziation = Verbindung

- Merksatz Assoziativgesetz / Eselsbrücke Assoziativgesetz: A-sso–z-iativgesetz: Anders solls zusammen.

- Anwendung bei: Aufgaben mit mehreren Additionen oder Multiplikationen (ggf. + Klammern)
  - - Einfache Formulierung: wenn die Aufgabe
      - nur Plusaufgaben oder nur Malaufgaben hat;
      - d.h. nur Strichrechnung oder nur Punktrechnung (einer Art)
      - keine Mischung von Rechenarten
      - d.h. nur Plus oder nur Mal

- Achtung:
  - - nicht wenn Plus und Minus in der Aufgabe sind
  - - nicht wenn Plus und Mal in der Aufgabe sind
  - - nicht wenn eine Mischung von Rechenarten in der Aufgabe steckt!!!!

- Gesetz:
  - - es ist egal, welche der Additionen oder Multiplikationen zuerst gemacht wird;
  - - die Klammern können gesetzt werden, wie man möchte.
      - Beispiel: 2 +(3 + 4) = (4 + 2) + 3 = 9
      - Beispiel: 2 x (5 x 7) = (2 x 5) x 7 = 70

- Achtung: NICHT, wenn Plus und Minus in der Aufgabe sind.

Achtung, Achtung, Achtung:

- Nicht bei Subtraktion oder Division!

- Auch nicht, wenn Addition und Multiplikation gemischt sind!

Onlineübungen

- Übungsaufgaben – einfach

- Übungsaufgaben – mittelschwierig

- Übungsaufgaben – schwierig

3. Distributivgesetz

= Klammergesetz

= Ausmultiplizieren von Klammern

Das WICHTIGSTE Gesetz!!!!

- Distributivgesetz: Verteilungsgesetz oder auch Klammergesetz

- Anwendung: bei der Multiplikation oder Division von Summen und Differenzen.

- Merksatz Distributivgesetz / Eselsbrücke Distributivgesetz: Di–str-i-bu-tivgesetz: Die Stränge bugsieren.

- Übersetzung: Distributiv = Verteilung

- Einfache Formulierung: wenn
  - - Plusaufgaben / Minusaufgaben in der Klammer
  - - und Malaufgaben oder Divisionsaufgaben vor der Klammer sind;
  - - d.h. Strichrechnung und Punktrechnung (mit Klammer) gemischt.

- Beispiel:
  - - (3+5) x 2 = 3×2 + 5×2 = 16
  - - (16 + 4) : 4 = (16 : 4) + (4:4) = 4 + 1 = 5

- Grundregel: Jedes Glied vor der Klammer wird mit jedem Glied in der Klammer multipliziert / dividiert!

- Übersicht gibt es um kostenlosen Download der Übersicht auf der Übungsseite.

Übungen

- Übungen und Aufgaben 1 – einfach, mittelschwierige und schwierige Aufgaben

- Übungen und Aufgaben 2 – einfach, mittelschwierige und schwierige Aufgaben

Distributivgesetz für Fortgeschrittene

Lernstufe 2: Das doppelte Distributivgesetz

Anwendung: wenn mehr als 2 Summanden (Terme, die miteinander multipliziert werden) in der Aufgabe sind.

Achtung: auch eine einzelne Zahl (im Beispiel unten: 3) kann ein Term sein. (Term: ein sinnvoller Ausdruck) Beispiel: 3 · (a + 5) · (b + 2)

Erklärung: das Beispiel hat 3 Terme:

- (a+5)

- (b+2)

Vorgehen: alle Terme müssen miteinander (aus-) multipliziert werden. Reihenfolge: in welcher Reihenfolge die Terme (aus-) multipliziert werden, ist egal.

Achtung: jeder Term muss mit jedem Term multipliziert werden!

Übungen und Aufgaben – mit Lösungen zu den Rechengesetzen:

Kommutativgesetz, Assoziativgesetz, Distributivgesetz

Die Grundlage: Punkt vor Strichrechnung

Die wichtigste Grundlage und Übung für die Rechengesetze ist die Regel der Punkt-vor-Strichrechnung. Übe diese daher unbedingt mehrfach, prüfe und vergleiche deine Lösung mit der angegebenen Lösung!