Termumformung
Termumformung: Definition und Grundlagen
Term: wird verwendet für alles, was eine Bedeutung trägt; in der Mathematik meint man: ‚Gebilde‘, die man ausrechnen kann.
Beispiel: x + y (x und y sind Variablen)
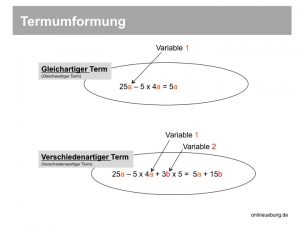
Gleichartige Terme – gleichwertige Terme: der Term enthält nur Variablen einer Art (z.B. ‚a‘). Diese kann man zusammenfassen.
- Beispiel: 2a + 3a = 5a
Verschiedenartige Terme – verschiedenwertige Terme: der Term enthält Variablen mehrerer Arten (z.B. ‚a‘ und ‚b‘). Solche Terme lassen sich nicht zusammenfassen!
- Beispiel: 2a + 3b = …
Termumformung: Terme kann man umformen und mit anderen Ausdrücken darstellen (um einfacher damit weiterrechnen zu können).
- Beispiel: Binomische Formel: (a+b)2 = a2 + 2*a*b + b2
Äquivalenzumformung
Bei der Äquivalenzumformung geht es darum, Gleichungen umzuformen, um einfacher damit weiterrechnen zu können.
Wichtige Begriffe der Äquivalenzumformung
- Gleichung: Eine Gleichung enthält auf beiden Seiten Terme, die nach einer Variablen umgeformt werden können. D.h. zwei Terme werden gleichgestellt.
- Variable: Unbekannte, Platzhalter für eine Zahl (z.B. a, b, c, x, …)
Wichtig: Bei der Äquivalenzumformungen haben beide Seiten der Gleichungen denselben Wert.
Wie formt man Gleichungen um?
- Ziel: (Die Variablen) auf eine Seite und die Zahlen auf eine Seite zu bringen bzw. zusammenzufassen (, um Terme zu vereinfachen)
- Vorgehen: Rechenoperation umkehren
- liegt eine Addition / Subtraktion vor, muss auf beiden Seiten (Zeichen: | ) subtrahiert / addiert werden.
- liegt eine Multiplikation / Division vor, muss auf beiden Seiten dividiert / multipliziert werden.
- Beispiel:
- 2x + 4 = 10 |-4
- 2x = 6 |/2
- x = 3
- Allgemein gilt: Multiplikation mit 0, lässt sich nicht umkehren, da man nicht durch 0 teilen darf!
- Beispiel: 0 * x + 7 = 15 |/0 ist nicht möglich
Termumformungsgesetze
Termumformungsregeln
- Regeln für die Termumformung:
- Klammern setzen: haben zwei Terme einen gemeinsamen Faktor, kann dieser ausgeklammert werden.
- Beispiel: 16x + 8 – 24 y = 4 (4x + 2 – 6y) – hier ist die ‚4‘ der gemeinsame Faktor.
- Klammern auflösen:
- Eine Klammer: Jedes Glied in der Klammer wird mit jedem Glied außerhalb der Klammer multipliziert.
- Beispiel: 3x + 7 (5 – 2x) = 3x + 7*5 – 7*2x = 3x + 35 – 14 x = 35 – 11x
- Mehrere Klammern: Jeder Term in der ersten Klammer wird mit jedem Term in der zweiten Klammer multipliziert.
- Beispiel: (3x + 5) (7x – 2) = 3x*7x + 3x*(-2) + 5*7x + 5*(-2) = 21x2 – 6x + 35x – 10 = 50x – 10
- Eine Klammer: Jedes Glied in der Klammer wird mit jedem Glied außerhalb der Klammer multipliziert.
- Minusregeln:
- Minus x Plus = Minus
- Minus x Minus = Plus
- Beispiel: (-3) * (-3)= +9
- Beispiel: – (-x) = +x
- Beispiel: − (x + y) = − x – y
- Beispiel: – (x – y) = (-x) + y
- Trick: man stellt sich eine 1 vor der Klammer vor:
- 6x – (4x – 5) =
- 6x – 1* (4x – 5) =
- 6x – 1*4x – 1 *(-5) =
- 6x – 4x + 5 =
- 2x + 5
- Fazit: Minus vor der Klammer dreht die Vorzeichen um – wenn man die Klammer auflöst.
- Klammern setzen: haben zwei Terme einen gemeinsamen Faktor, kann dieser ausgeklammert werden.
Übersicht
- Erklärvideo: Was ist ein Term, was ist Termumformung, …
- Erklärvideo: Rechnen mit Variablen
- Quiz: Terme
Gleichartige Terme umformen
Gleichartige Terme sind Terme mit nur einer Variablen.
- Erklärvideo: Gleichung umformen
- Musterberechnung: Gleichung umformen
- Onlineübung (als Millionenspiel)
Verschiedenartige Terme umformen
Verschiedenartige Terme sind Terme mit mehreren, verschiedenen, Variablen.
Terme oder Gleichungen aufstellen
Textaufgaben zur Termaufstellung

